Two sample goodness of fit test (k=5)
 
  

 



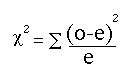
The equation measures how closely the responses in two distributions match.

Enter the frequency data from the data sheet directly into the webulator below.

Responses Sample 1 Sample 2 Row Sums
Option 1
Option 2
Option 3
Option 4
Option 5
Sum of Sample 1 responses Sum of Sample 2 responses Grand Total
Formula for column 1 Expected Responses
Sample 1		 Formula for column 2 Expected Responses
Sample 2
(row1 sum * col1 sum)
grand total 		(row1 sum * col2 sum)
grand total
(row2 sum * col1 sum)
grand total 		(row2 sum * col2 sum)
grand total
(row3 sum * col1 sum)
grand total 		(row3 sum * col2 sum)
grand total
(row4 sum * col1 sum)
grand total 		(row4 sum * col2 sum)
grand total
(row5 sum * col1 sum)
grand total 		(row5 sum * col2 sum)
grand total

Chi Computations Sample 1 Sample 2
(observed- expected)2
expected
(observed- expected)2
expected
(observed- expected)2
expected
(observed- expected)2
expected
(observed- expected)2
expected
Sum of (observed- expected)2
expected

The important value from this Webulator is the chi-square score. The chi-square score is the sum of (observed score minus expected score)2 divided by the expected. As show in the following formula.

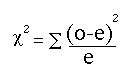
The computed score is referred to as the chi-square observed. After computing the chi-square observed value, determine the chi-square critical score from a table of chi square values. The chi-square critical score presented in these examples represents what we should expect to observe for two sample distributions each with five possible responses. The critical value is determined by computing the “degrees of freedom” for our response set.

The computation of the degrees of freedom is:

degrees of freedom = (number of rows - 1 )(number of columns -1)

degrees of freedom = (5-1) x (2-1)

degrees of freedom = (4) x (1)

degrees of freedom = 4

and the “chi-square critical value” for degrees of freedom of “4”

at p<0.05 = 9.49

If the “chi-square observed value ” is › the “chi-square critical value of 9.49”, we would reject the null hypothesis and state that the two distributions ARE NOT EQUAL. However, if the “chi-square observed value ” is ‹ the “chi-square critical value of 9.49”, we would ACCEPT the null hypothesis and state that the two distributions ARE EQUAL.

Computations for Chi Square are discussed in several texts including:

Fleiss, J., (1981). Statistical methods for rates and proportions, (2nd ed). Toronto: John Wiley and Sons.

Freedman, D., Pisani, R., Purves, R., Adhikari, A., (1991). Statistics. New York: Norton and Company.

Freund, J.E., and Simon, G.A., Statistics A First Course, New Jersey, Prentice Hall, page 66-67,1991.

Saunders, D.H., Statistics A Fresh Approach,Toronto, MGraw-Hill Publishing Company, 1990.

Hirsch, R.P., and Riegelman, R.K., Statistical First Aid: Interpretation of Health Research Data, Boston, Blackwell Scientific Publications, page 73-75,1992.

Knapp R.G., and Miller, M.C., Clinical Epidemiology and Biostatistics , Baltimore, Williams and Wilkins, 1992.

Click here to return to the Webulator Menu Page
For more information, please contact:

Professor William J. Montelpare, Ph.D.,
Margaret and Wallace McCain Chair in Human Development and Health,
Department of Applied Human Sciences, Faculty of Science,
Health Sciences Building, University of Prince Edward Island,
550 Charlottetown, PE, Canada, C1A 4P3
(o) 902 620 5186


Visiting Professor, School of Healthcare, University of Leeds,
Leeds, UK, LS2 9JT
e-mail wmontelpare@upei.ca
Copyright © 2002--ongoing [University of Prince Edward Island]. All rights reserved.