3 x 3 Contingency Table for Chi-square Analysis
 
  

 


The equation below is the basic equation for the chi square test.

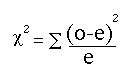
Use the Chi square Webulator to enter your data and compute the Chi-square observed score.


Variable 1
Condition 1
 Condition 2
 Condition 3
 Row Sums
Variable 2
Condition 1
Variable 2
Condition 2
Variable 2
Condition 3

Sum of
Column 1		 Sum of
Column 2 		Sum of
Column 3		 Grand
Total

Formula for column 1 Expected Responses
Column 1 		Formula for column 2 Expected Responses
Column 2 		Formula for column 3 Expected Responses
Column 3
(row1 sum × col1 sum)
grand total 		(row1 sum × col2 sum)
grand total 		(row1 sum × col3 sum)
grand total
(row2 sum × col1 sum)
grand total 		(row2 sum × col2 sum)
grand total 		(row2 sum × col3 sum)
grand total
(row3 sum × col1 sum)
grand total 		(row3 sum × col2 sum)
grand total 		(row3 sum × col3 sum)
grand total

Chi Square Computations Column 1 Column 2 Column 3
(observed- expected)2
expected
(observed- expected)2
expected
(observed- expected)2
expected
Chi square formula Chi-Square= 


The computed score is referred to as the chi-square observed. After computing the chi-square for the observed scores we next determine the chi-square critical score which represents the chi-square for the expected population.
The chi-square critical score for a three by three frequency table is determined by computing the “degrees of freedom” for our response set.

The computation of the degrees of freedom is:

degrees of freedom = (number of rows - 1) x (number of columns -1)

degrees of freedom = (3-1) x (3-1)

degrees of freedom = (2) x (2)

degrees of freedom = 4

and the "chi-square critical value” for degrees of freedom of "4” at p<0.05 = 9.49

Our null hypothesis in this scenario is that there is no association between the row and column variables. If the "chi-square observed value” is › the "chi-square critical value of 9.49” then we would reject the null hypothesis and state that there is an association between the row and column variables. However, if the "chi-square observed value ” is ‹ the "chi-square critical value of 9.49”, we would ACCEPT the null hypothesis and state that the distributions ARE EQUAL.


Click here to return to the Webulator Menu Page
For more information, please contact:

Professor William J. Montelpare, Ph.D.,
Margaret and Wallace McCain Chair in Human Development and Health,
Department of Applied Human Sciences, Faculty of Science,
Health Sciences Building, University of Prince Edward Island,
550 Charlottetown, PE, Canada, C1A 4P3
(o) 902 620 5186


Visiting Professor, School of Healthcare, University of Leeds,
Leeds, UK, LS2 9JT
e-mail wmontelpare@upei.ca
Copyright © 2002--ongoing [University of Prince Edward Island]. All rights reserved.